When can machines learn? (illustrative + technical)
learning is impossible?
No free lunch: NFL定理最重要的寓意,是让我们清楚地认识到,脱离具体问题,空泛地谈论”什么学习算法更好“毫无意义,因为若考虑所有潜在的问题,则所有的算法一样好. 要谈论算法的相对优劣,必须要针对具体问题;在某些问题上表现好的学习算法,在另一问题上却可能不尽如人意,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性作用.
probability to the rescue
inferring something unknow:
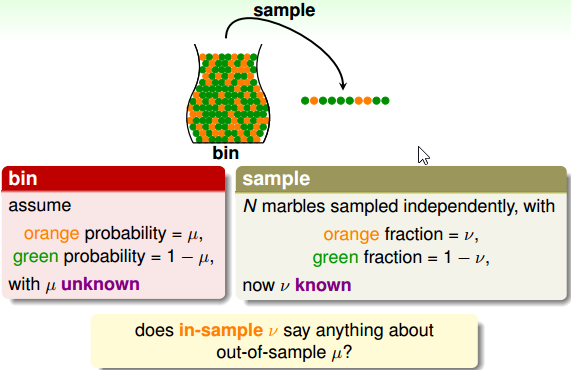
在不知道瓶子中各种颜色弹珠数量的前提下,考虑一个瓶子中橘色弹珠的比例。
解决方式: sample:
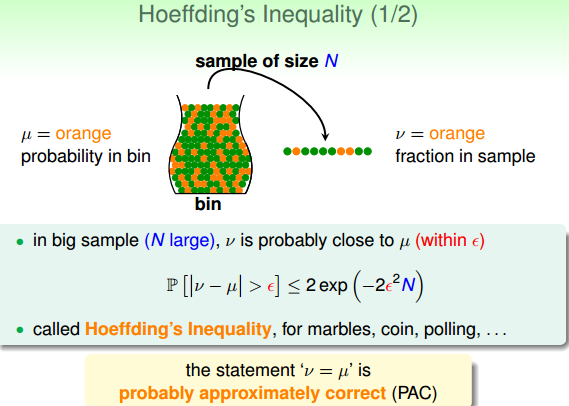
霍夫定理:
connection to learning
将下图中的一颗一颗的弹珠,想象为一个一个的样本x, 如果 hypothesis h 与 target f 对样本 x 表现不一致,则将弹珠染为橘色的,否则染为绿色的。
假设现在有一个固定的 h 在手上,则就可以按照上面的规则将弹珠染为橘色或者绿色。
从瓶子中将染好颜色的弹珠抓出来,比如抓出100个弹珠,就相当于抓取出了100个样本 x 出来了,这个做的好处是可以检验 h 在数据集 D 上的表现,有多少样本 x 与 f(x) 与真实值 y 变现的不同。
这样就能从看见的资料中,衡量 hypothesis h 与 target f 之间的偏离程度。

个人理解,林老师想表达的意思是:瓶子中的弹珠就像整个数据集,我们没有办法将整个瓶子的弹珠倒出来检查一遍颜色(即不能在整个数据集上验证 hypothesis h ),因此采用独立同分布的方式从瓶子中取出一部分弹珠(即在一部分数据集上验证 h),来评价 h 与 f 之间的相似程度。
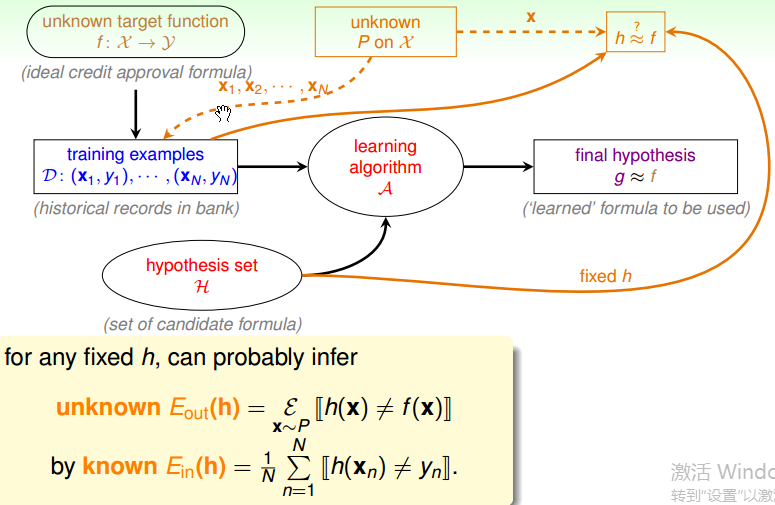
下图中,有很多的原件,其中 unknown P on X(相当于瓶子),以一定的几率从瓶子中取样会用在两个地方(即图中的两个虚线),一个是 training examples,另一个是 h ≈ f,其中 Ein 表示 in-sample(即从瓶子中取出来的弹珠,手上的弹珠),Eout 表示 out-of-sample(即没有采用出来的弹珠,手上以外的瓶子里面的弹珠),通过 Ein 能够根据霍夫不等式求出 Eout。
- 霍夫不等式对所有的 N 与 ε 都是正确的
- 霍夫不等式不依赖于 Eout, 即不需要知道 Eout,也不需要 f 和 P.
- 根据 probably approximately correct(PAC) 定理, Ein = Eout。这个保证来源于Ein 和 Eout 都是从分布 P 中产生的。

如果在组合的 h 中, Ein(h) 足够小, learning algorithm A 拿出来一个 h 做为 g => ‘g = f’ PAC。
如果只有一个 hypothesis h,怎么来验证 g 与 f 是否接近呢? 首先可以将唯一的 h 作为 g, 然后从 P 中抽取一部分样本,来验证 g 与 f 之间是否接近。
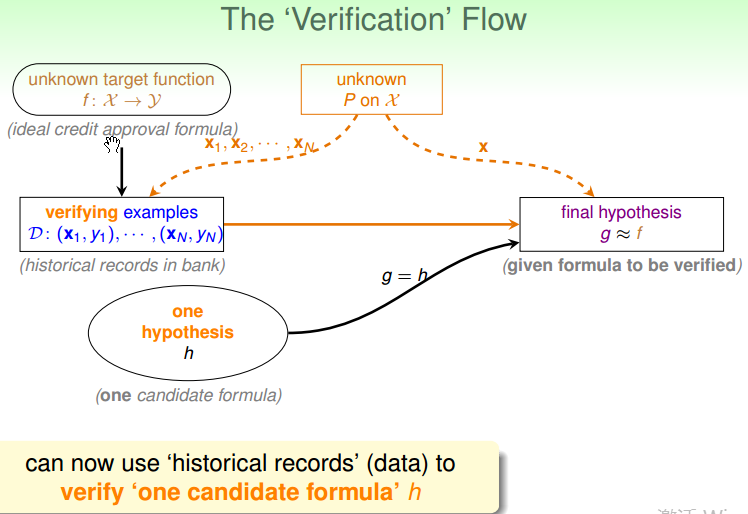
connection to real learning
上面假设了只有 1 个 hypothesis h 时候的验证方式,假设现在有多个 hypothesis h,应该怎么处理呢?
例如下图,有 M 个 hypothesis,其中 hM 在 Ein(hM) 中表现都是正确的(即训练集的误差为0),你要不要选 hM。
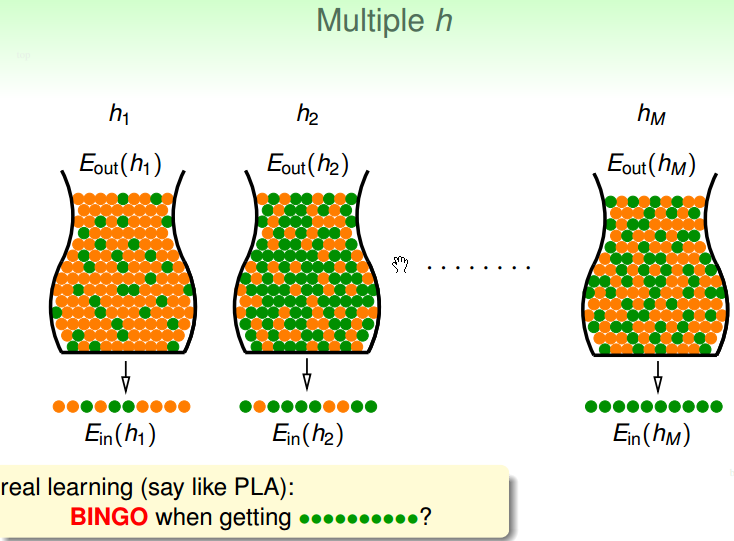
图中也形象的说明了, h2 中的绿色弹珠最对,即 h2 在所有数据上误差最小。因此,如果选择 hM 尽管 Ein(hM) 全是正确的(即训练集误差为0), 但是 hM 确不是最好的 g(过拟合了)。
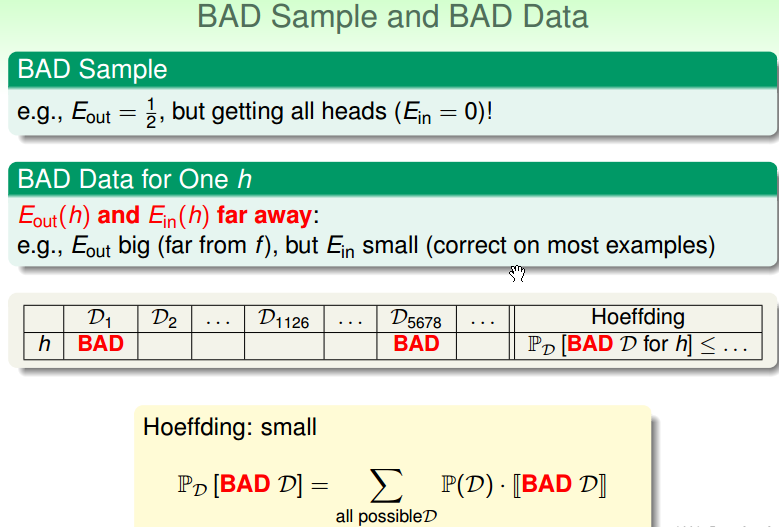
Bad sample (不好的抽样): Ein 与 Eout 非常不接近。 hypothesis 变大的时候(即 h 变多的时候),是会加大 Bad sample 的概率。例如,只有 1 个硬币(即只有1个 hypothesis),丢5次全为正面的概率为 1/32,但是如果有 150 个硬币(即有150个 h),其中有5次全为正面的概率为 1 - (31/32)150。
霍夫不等式给出了 Bad sample 的概率为,下图是只有一个 h 时候的概率,说明 Bad sample 的概率很小:
但是,如果有多个 h 的时候,Bad sample 的概率就变大很多:
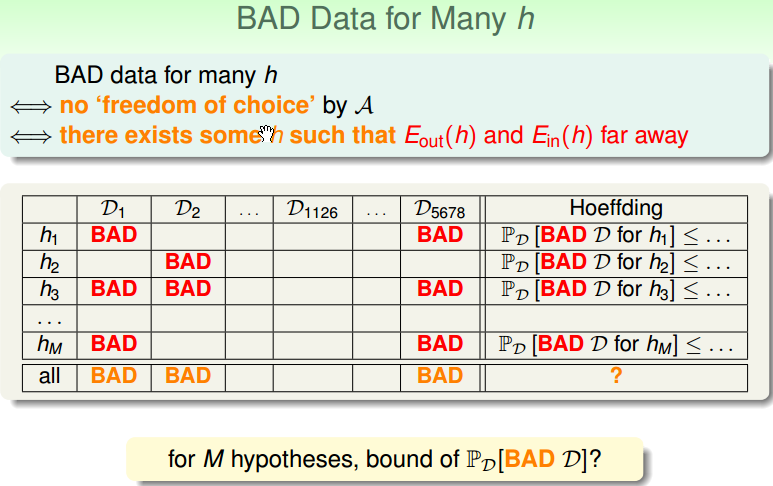
从上图可以看出,霍夫不等式是对一个一个的 h 的保证,即每行的 Bad sample 的概率都很小,但是 learning algorithm A,是从多个 h 中选出一个做为 g(即通过资料 D1 ,从 h1 到 hM 中,选择一个 g),即每列遇到 Bad sample 的概率。
对于 M 个 h,遇到 Bad Data 的上限为:

上面的图片也是表明了,选择 g 的原则为,使 Ein(g) 尽量小。
下图是一个学习的过程,即主要由两点组成。
- if |H| = M 是有限的,并且样本数据个数 N 足够大,无论算法 A 怎么选择到的 g, 都能保证 Eout(g) ≈ Ein(g)。
- if 算法A找到一个 g,使得 Ein(g) ≈ 0,则 PAC 能够保证 Eout(g) ≈ 0.
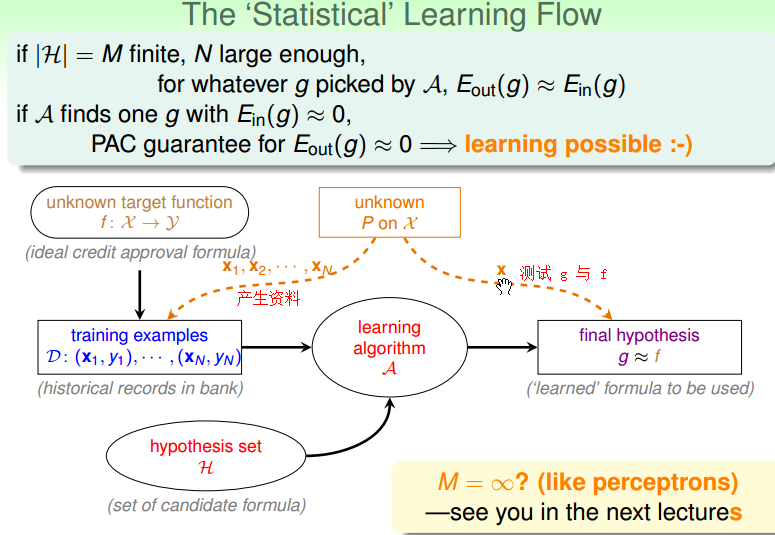
本节主要解决了,在有限的 hypothesis h 的条件下,机器学习有可能做到的证明。下面的几个将处理在无限的 hypothesis h 的条件下,机器学习的证明。