When can machines learn? (illustrative + technical)
Why can machines learn? (theoretical +illustrative)

Recap and preview
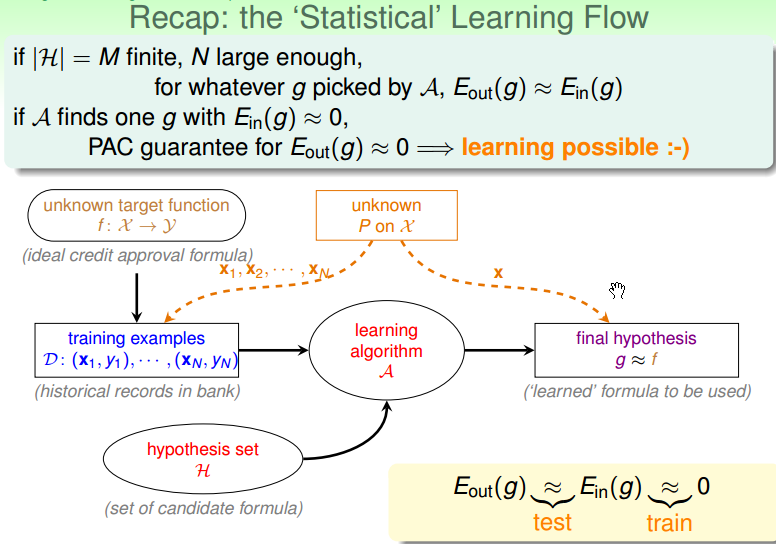
复习:整个 learning 的流程图如下图所示, learning 从资料 training examples 出发,通过资料以及 hypothesis set,最终从里面选择了一个最终的 hypothesis g(assumption: 训练的资料和最终测试 hypothesis 方法,都来自于同样的一个 distribution)。
如果训练集和测试集都来自于同样的一个分布,且 hypothesis set 的集合是有限的,则对于 learning algorithm A 选择的任意一个 g,都可以保证 Eout(g) ≈ Ein(g)。
如果 learning algorithm A 找到一个 g, 使得 Ein(g) ≈ 0,PAC 能够保证 Eout(g) ≈ 0。(这使得机器学习时间可能的事情)。
这里的两个重要假设是:① 训练集和测试集都来自于同样的一个分布;② PAC 定理。
下图总结了前面的4节课中的主要内容:
- 第一节课,期望找到一个 g,使得 g 与 f 很接近。
- 第二节课,期望找到使 Ein(g) ≈ 0 的方法。
- 第三节课,了解了批次数据、监督学习以及二元分类的情况(PLA)。
- 第四节课,将 Eout(g) ≈ Ein(g),连接了一起。

这里将 learning 拆分为了两个问题,如下图所示:

提出问题:M(hypothesis set 的大小) 在上述两个问题中扮演者什么样的角色?
Trade-off(权衡) M:
这里会有两种情况:
- M 很小的时候:①Yes -> 坏事情 p[BAD] 发生的概率如下图所示,因此,当 M 很小的时候,坏事情(即 Eout(g) 和 Ein(g) 不接近)发生的概率就很小。②No -> 当 M 很小的时候,可以选择的算法就很小,未必能够找到一个 g 使得 Ein 足够小。
- M 很大的时候:①No -> 。②Yes -> 选择更多了。

因此,如果 M 太大的话,未必是一件好事。
对比 M 是有限的还是无线的两种情况:

下面的问题也很有意思,他保证了要想 Eout(g) 和 Ein(g) 接近的话,至少需要的数据量。

Effective number of lines
复习:下面复习下 M 的来源,考虑 BAD events 的定义为 Eout(g) 和 Ein(g) 相差很远(大于 ε)的如下图所示,当有 M 个可用选择的 f,则可以使用联结的形式将这些 f 联结在一起。

下面的问题是,如果 M 的无限的,怎么办呢?(Uniform Bound Fail?)
现在想,如果有两个比较接近的 hypotheses h1 ≈ h2(比如两条比较接近的线),这两个比较接近的 h1 、 h2 的 Ein是一样的,Eout 也很接近。

这种坏事情是互相叠起来的,像上图中的右边的 B1, B2, B3 所示。但是,我们在使用 Uniform Bound 的时候,并没有考虑叠起来这件事情,所以造成上限是一个 over-estimating。
下面要做的事情就是找出这些坏事情重叠的部分:
- 第一步,能否将无限多的 hypothesis set,分为有限多个类?
- 如何分类?

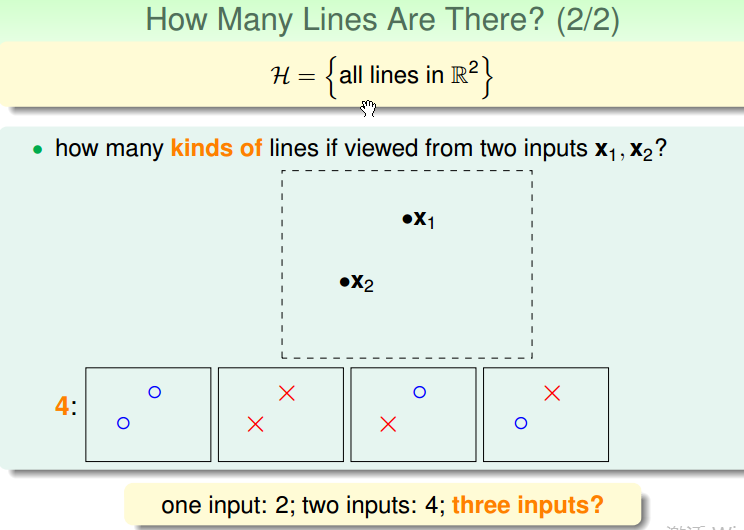
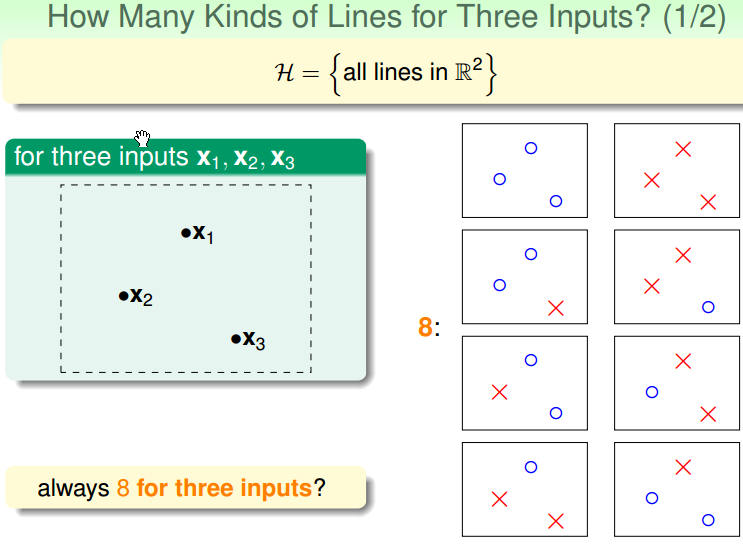
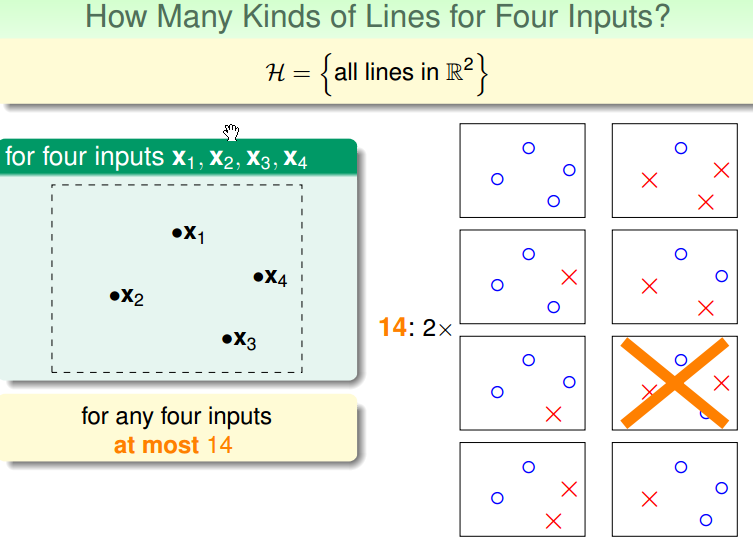
在平面中的点和线而言,以将点划分为不同的类为区分:
- 1个点,有 2 种线
- 2个点,有 4 种线
- 3个点,最多有 8 种线
- 4个点,最多有 14 种线
如果将输入的点以线分开的话,得到的有效的线的数量是有限的。
使用 effective(N) 来代替 M。 effective(N) << 2N。N 代表 N 个点(即 N 个样本)。
如果只从输入的点看的话,那么得到线的种类是有限的,把这种有效的线叫做: Effective Number of Lines。

就算有无限多条线 M,如果能够将无限多条线分为 effective(N), 比 2N 小很多的话,我们就可以保证可能学的到东西。
Effective number of hypotheses
Dichotomies: Mini-hypotheses
下面想象有这么一个 hypothesis,它将 X 空间分为 {x, o},假如有 N 个点(x1, x2, … , xN)的话,这 N 个点产生了几种{x, 0}组合可能性,将这种组合叫做 Dichotomy。
- a dichotomy(二分的意思):
- 下面想看看一个 hypothesis set 可以做出多少种 dichotomy 出来,例如其中一个 dichotomy 将所有的点都分为 o。
- H(x1, x2, … , xN) :将所有的 dichotomy 放在一起,形成一个集合,用 H(x1, x2, … , xN) 表示。这是 dichotomies,而不是原来的 hypothesis set。
- 具体的情况,如下图所示:hypotheses H 的大小最多有无限多个,而 dichotomies H(x1, x2, … , xN) 的上限为 2N。
- 接着用 |H(x1, x2, … , xN)| 的大小来代替 M.

Growth Function
其实,dichotomies size |H(x1, x2, … , xN)| 的大小,是取决于先选好的 (x1, x2, … , xN)(想下前面当有3个点时,可能有 8 种组合,在一条线上时有6种组合)。
如果想要剔除掉对先选好的点(即对 X 的依赖),就算下最终最大有几种就可以了:
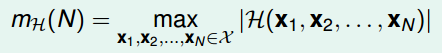
将最大的 dichotomies size 记录为 mH(N),并将 mH(N) 成为 Growth Function(成长函数)。Growth Function 的输出一定是有限的,因为最多为 2N。

下面要解决的问题是,如何计算 Growth function?
Growth Function for positive rays
输入:一维的实数,
hypothesis: 大于阈值为正,小于阈值的为负。
给N个点,最多可以切出多少不一样的 dichotomy? 可以有 N+1 种 dichotomy。即成长函数为:mH(N) = N + 1

核心目标是:利用成长函数 mH(N) 来代替 M。
Growth Function for positive intervals
mH(N) = 1/2 * N2 + 1/2 N + 1
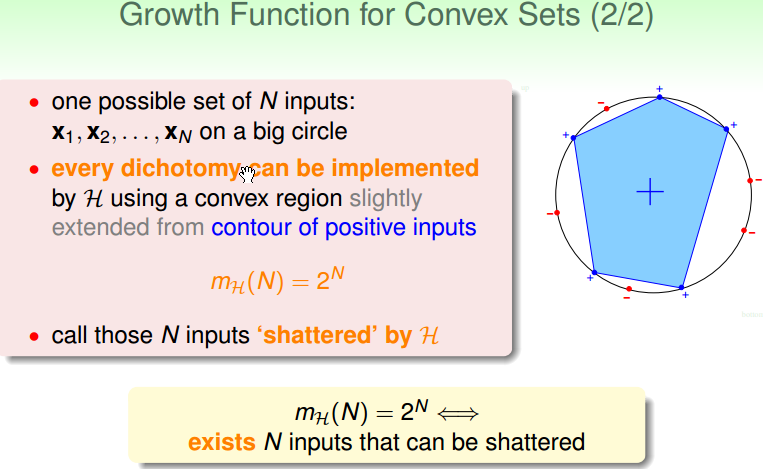
Growth Function for convex sets
mH(N) = 2N,即 “shattered”, 即这 N 个点,被下面这种 hypothesis 打散了。
四个不同的成长函数为:

Break point
成长函数第一个看起来有一些希望的点在哪里?把这个点叫做 Break point。例如在 perceptrons 中,3个点的时候有8种情况,4个点的时候有14种情况,将第4个点叫做 perceptrons 的 break point。
从 k 是 break point 的时候,k 以后都是 break point。

2D perceptrons 的 break point 为:4
break point 和成长函数有一定的关系,见下图的左下角。
