When can machines learn? (illustrative + technical)
Why can machines learn? (theoretical +illustrative)
希望成长函数 mH(N) 来代替实际的 M ?
Restriction of Break Point
growth function mH(N): max number of dichotomies(即最多能够产生几种不同的 xx 或 oo)。即 hypothesis set 在 N 个点上,最多能够产生多少种 dichotomy.
几种不同类型的成长函数形式:

上面的 2D perceptrons, 虽然不知道成长函数是什么样的类型,但是可以知道 break point 为4.
下面一种情形为:当最小的 break point k = 2 时,当有 1个点,2个点,3个点的情形:可以证明,当有1个点 N = 1时,可以被成长函数 mH shatter(打散),当有2个点的时候,不能够被 shatter ,最大的 dichotomies 小于4,当 N = 3 时,不能被 shatter,最大的 dichotomies 等于4.

小练习:
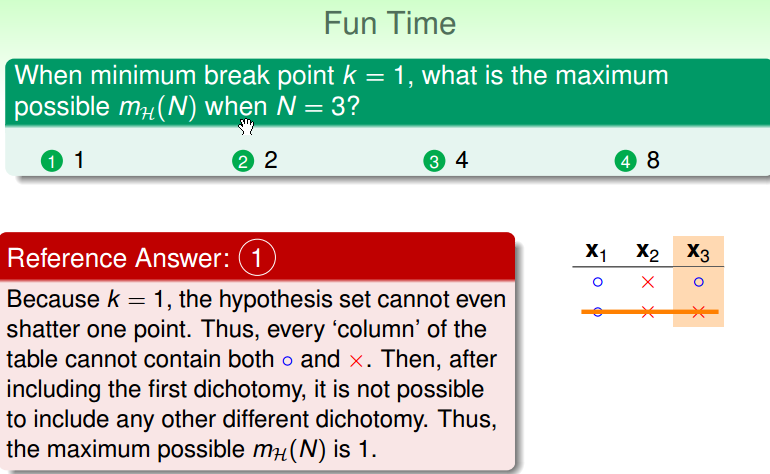
Bounding Function: Basic Cases
bounding function B(N, k): maximum possible mH(N) when point = k。这个成长函数在 K 那边漏出一线曙光,是它的 Break point, 那这个成长函数最多有多少种 dichotomy 的可能?
限制条件: 最大长度为 N 向量的(o, x),然而 ‘no shatter’ 任何 长度为k 的子向量。就是不希望看到 2k 的组合,即不能出现 shatter,不能将 k 个点,统统都 ko 掉。
例如:上线函数 B(N, 3) 的地方边界有两种:① positive intervals(k=3);② 1 D perceptrons(k=3)。即不去考虑 positive intervals 以及 1 D perceptrons 的成长函数,而是直接考虑他们的上线:B(N, 3)。
接下来就先证明,上线函数 bounding functions 是像多项式那样的成长。
new goal: B(N, k) ≤ ploy(N) ?
现在的 B function 有两个参数,一个是 N(有几个点), 一个是 K(一线曙光发生的地方).
前面我们知道的情形:
- B(N, 1) = 1
- B(2, 2) = 3(maximum < 4)
- B(3, 2) = 4(‘pictorial’ proof previously)
- 容易知道,当 N < K 时,B(N, k) = 2N
- 当 N = K时,B(N, k) = 2N - 1
B function(实际是成长函数的上线) 查表为:
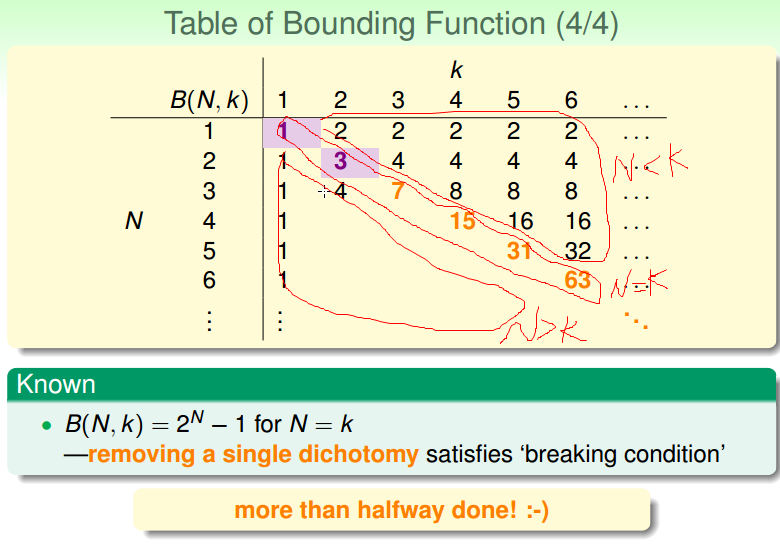
Bounding Function: Inductive Cases
下面开始填上面的 B function 的左下角的部分。