入门
开始时,作者讲了一些小典故,非常有意思:
数千年来,预测一直吸引着人们。古巴比伦的预言家们可以基于蛆在腐烂的绵羊肝脏中的分布预测未来。在公元前300年,想要预知未来的人们会前往希腊的德尔菲祈求神谕,神谕会在被乙醚蒸汽陶醉的情况下给出她的预言。预言家们在康斯坦丁大帝的统治下经历了一段艰难的时期,康斯坦丁大帝在公元357年颁布了一项法令禁止任何人“去咨询占卜者、数学家或预言家,对预言未来的好奇将被永远禁止。”1763年英国颁布了一项相似的禁令:通过预测骗取钱财将被判作犯罪,其刑罚是判处三个月的狱中的苦役。
什么是可以被预测的
事件(或数量)的可预测性取决于以下几个因素:
- 我们对它的影响因素的了解程度;
- 有多少数据是可用的;
- 预测是否会影响我们试图预测的事物。
预测、计划和目标
该小节讲述了预测、目标以及计划之间的关系。
预测:它是指在考虑到所有可用信息的前提下,包括历史数据和可以影响预测的任何未来事件的知识,尽可能准确地预言。
目标:它是指你想要发生的事情。目标理应与预测和计划联系在一起,但是这并不经常发生。很多时候,设定目标时没有任何如何去实现这些目标的计划,也没有目标是否切合实际的预测。
计划:它是对预测和目标的回应。计划包括制定使得你的预测符合你的目标的适当行动。
而预测又可以分为短期预测、中期预测、长期预测等,具体预测取决于特定的应用场景。
决定预测什么
- 决定预测什么:
- 用于每条产品线或一组产品?
- 用于每条产品线或一组产品?
- 每周数据、月度数据或年度数据?
- 考虑预测的前景时段:
- 需要提前1个月,提前6个月还是提前10年预测?
- 预测需要多频繁?需要经常进行的预测, 最好是使用自动化系统, 而不是需要仔细人工操作。
在制定合适的预测方法之前, 预测者大一部分的时间将用于寻找和整理可用数据。
预测数据和方法
在大程度上,什么数据是可用的决定了适合什么合适的预测方法。
定性预测:
- 如果没有可用的数据,或者如果可用的数据与预测无关,那么应该使用定性预测方法。
在满足以下两个条件的时候可以使用定量预测 :
- 关于过去的数字化信息是可以用的;
- 有理由假设过去的一些模式会在未来延续下去。
大多数定量预测问题都使用时间序列数据 (按时间间隔定期收集) 或横截面数据 (在一个时间点收集)。在本书中,我们关注预测未来的数据,并且我们主要专注于时间序列领域。
时间序列数据样例包括:
- IBM每日股票价格
- 每月降水量
- 亚马逊季度销售结果
- 谷歌年度利润
最简单的时间序列预测方法只用了预测变量的信息,而不去寻找影响预测变量的因素。因此,这些方法可以推断趋势部分和季节性部分,但是它们会忽略掉所有其他的信息,如营销计划,竞争对手活动,经济状况变动等。
用于预测的时间序列模型包括分解模型,指数平滑模型,ARIMA 模型。这些模型分别在章节 6,7 和 8 中进行了分析探讨。
预测变量与时间序列预测
以预测夏季每小时用电需求量为例:
- 解释模型
ED = f(当前气温,经济实力,人口当日时间,星期几,误差)
这种关系并不确切–总会有不能由预测变量决定的电力需求变化。右侧的“误差”项表示随机波动和没有被包括在模型中的相关变量的影响。我们将它称之为“解释模型”,因为它帮助解释电力需求变化的原因。
- 时间序列模型
t 表示当前的时间, t+1 表示下一个小时,t−1 表示前一个小时,t−2 表示前两个小时,以此类推。此处,对未来的预测是基于变量的过去值,而不是基于可能影响系统的外部变量。同样,右侧的“误差”项允许随机波动和不包含在模型中的相关变量的影响。
- 混合模型:结合了上述两种模型的特点
解释模型非常有用,因为它包含了有关其他变量的信息,而不仅仅是要预测的变量的历史值。但是, 预测者可能选择时间序列模型而不是解释性或混合模型的原因有多种:
- 这一系统可能不被理解,即使被理解,也很难衡量被认为应该管理行为的关系。
- 其次,有必要知道或预测各种预测因子的未来价值, 以便能够预测有意义的变量, 但是这可能太难了。
- 第三, 可能主要只是关注预测会发生什么,而不知道为什么会发生。
- 最后,时间序列模型可以提供比解释或混合模型更准确的预测。
在预测中使用的模型取决于可用的资源和数据、模型的准确性以及预测模型的使用方式。
案例学习
该小节,作者讲了4个案例,有以下几个特点:
- 时间序列数据显示出一系列模式,其中一些带有长期趋势,一些带有季节变动,还有一些两者都不具备。
- 几乎每种药品的销售量数据都包含长期趋势和季节变动模式。很多药品的销量会因药品补贴政策的变化而突然上升或下降,对很多药品的津贴支出也会因出现低价可替代药品而突然发生变化。(因此,我们需要寻找到一种能够对包含长期趋势和季节变动因素的数据进行预测的方法,使得该方法不仅可以对潜在模式下的突然变动进行稳健预测,同时能够处理大样本的时间序列数据。)
- 一群专家正在预测汽车转售价格。他们认为统计模型的建立会对他们的生计造成威胁,因而在提供信息方面不合作。尽管如此,该公司还是给我们提供了大量的车辆和汽车转售价格的历史数据。
- 航空乘客人数会受到学校假期、重大体育赛事、广告活动、竞争行为等影响。一般情况下,澳大利亚不同城市的学校假期不会同时出现,体育赛事有时也会从一个城市转移到另一个城市。在历史数据相应期间发生过一场关键飞行员的罢工运动,其间几个月都没有相关航线运行,一条新的低价航线推出后也惨遭失败。在历史数据期间的末尾,航空公司将一些经济舱座位重新改造为商务舱和头等舱座位,然而几个月后,座位安排重新恢复到原来的状态。
预测过程的主要步骤
一个预测过程通常包括五个基本步骤。
定义问题
通常这是预测中最困难的步骤。要准确定义这个问题,需要了解怎样运用预测方法,谁需要这个预测,以及预测效果如何满足需要这个预测的机构。预测人员需要花费一定时间与所有参与收集数据、维护数据库和使用这个预测对未来进行规划的人沟通。
收集信息
一般至少需要两种信息收集方式:(a) 统计数据,(b) 收集数据和进行预测方面专家的积累经验。通常情况下,要获得足够多的历史数据以构建良好的统计模型是很困难的。在这种情况下,可以使用 第4节 中的判断预测方法。有时候,陈旧数据会因相应数据发生结构变化而失效,因而我们一般只选择使用较新的数据。然而,一个好的统计模型可以处理系统中的结构变化,因此不要轻易丢弃好的数据。
初步(探索性)分析
总是以图形开头,观察思考以下几个问题:
- 有一致的模式吗?
- 有明显的长期趋势吗?
- 季节性重要吗?
- 是否有证据表明商业周期存在?
- 数据中是否包含需要专业知识解释的异常值?
- 用于分析的变量之间的相关性有多强?
目前已经开发了各种工具来帮助进行这种分析。这些将在章节 2 和 章节6中讨论。、
选择及拟合模型
最佳模型的选择取决于历史数据的可用性、预测变量与各解释变量之间的相关性,以及预测的使用方式。比较两个或三个潜在的模型是很常见的。每个模型本身都基于人为提出的一组假设(显式和隐式)而建立,通常包含一个或多个参数,这些参数必须使用已知的历史数据进行估计。我们将讨论回归模型(章节 5)、指数平滑方法(章节 7)、Box-Jenkins ARIMA模型(章节 8)、动态回归模型(章节 9)、分层预测(章节 10),以及其他各种方法,包括计数时间序列、神经网络和章节 11中的向量自回归。
使用及评估预测模型
一旦模型及其参数确定后,该模型就可以用来进行预测。模型的预测效果只有用于预测的数据得到之后才能得到正确的评价。目前已经开发了许多方法来评估预测的准确性。在使用和进行预测时会存在很多组织结构问题。对其中一些问题的简要讨论将在章节 3 中给出。
统计预测观点
我们试图预测的东西是未知的(或者我们不能预测它),所以我们可以把它想象成一个随机变量。
例如,下个月的总销售额可能会有一系列的可能值,直到月底我们把实际销售额加起来,我们才知道这个值会是多少。所以在我们知道下个月的销售情况之前,这是一个随机的变量。
因为下个月时间节点比较近,我们通常清楚销售量大概是多少。如果我们预测明年同一个月的销售情况,可能的销售量变动就会较大。在大多数预测情况下,随着事件的临近,预测对象的相关变动较小。换句话说,预测的越早,预测结果越不稳定。
我们可以想象许多可能性,每一个都为我们将要预测的事物带来不同的影响。下图是1980年到2015年澳大利亚的国际游客总数以及2016至2025年的10个可能的预测值。
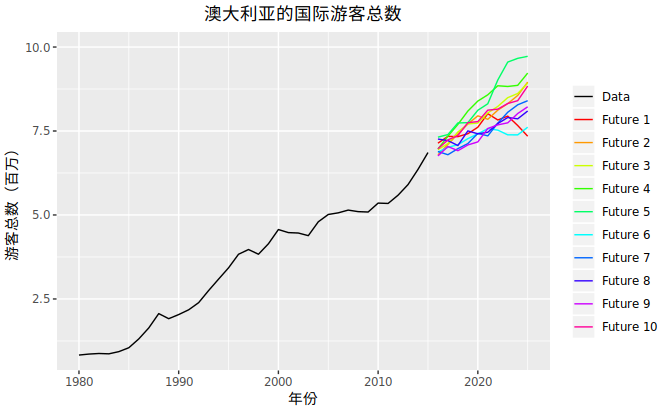
用上面10个预测来加权,应该效果不错。
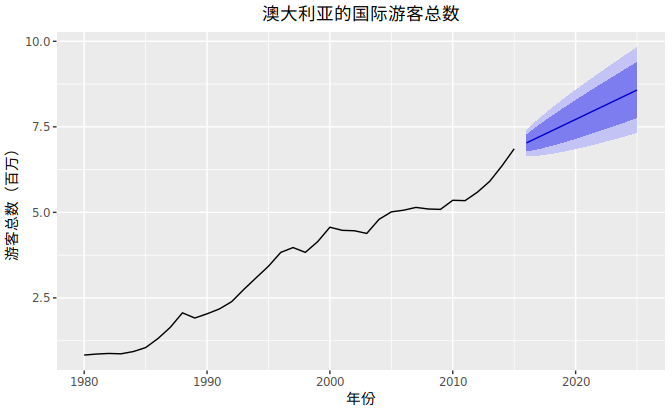
我们进行预测的过程实际是寻找随机变量可能取值范围内的中间值。通常情况下,预测会伴随着一个预测区间,给出一个随机变量具有较高概率的范围值。例如,95%的预测区间包含一系列的值,这个预测区间包含实际未来值的概率为95%。
我们通常会给出这些预测区间,而不是图 1.2 中显示的单个可能的预测值。下面的图表显示了未来澳大利亚国际游客的80%和95%的预测区间。蓝线是可能的预测值的平均值,我们称之为“点预测”。
使用下标 t 作为时间。例如, $ y _{t} $ 表示时间 t 对应的观察值。假设将观察到的所有信息表示为 T,目标是预测 $ y _{t} $ .此时,我们将 $ y _{t} | T $ 表示为“给定已知 T 情况下的随机变量 $ y _{t} $ ”。这个随机变量取值的概率测度称为 $ y _{t} | T $ 的 “概率分布”。在预测中,我们称之为“预测分布”。
每当我们谈到“预测”时,通常指的是预测分布的平均值,用 $ \hat{y _{t}} $ 来表示 $ y _{t} $ 的预测值,这意味着 $ y _{t} $ 所有可能取值的均值包含了我们所有已知的信息。有时我们将使用 $\hat{y _{t}} $ 来表示预测分布的‘中位数’(或中间值)。
明确指出我们在进行预测时使用的信息是很必要的。例如,我们使用 $ \hat{y _{t}} $ 表示在已知观测值 $ (y _{1},…,y _{t-1}) $ 的情况下 $ y _{t} $ 的预测值。类似地,我们使用 $ \hat{y _{T+h|T}} $ 表示在已知观测值 $ (y _{1},…,y _{T}) $ 的情况下 $ y _{T+h} $ 的预测值(即考虑时间 T 之前所有观测值的h步预测).
拓展阅读
- Armstrong (2001) 涵盖了整个预测领域的内容,每个章节都由不同的专家撰写。文章部分观点非常武断(我们并不同意其中的观点),但在处理预测问题上有很多优秀的一般性建议。
- Ord, Fildes, and Kourentzes (2017) 是一本预测教材,涵盖了与本书相同的部分,但重点不同,它不关注任何特定的软件环境。这是由三位有着几十年经验的权威预测专家撰写的。
时间序列图形
对于任何数据分析工作而言,其首要任务是数据可视化。图示化数据可以清晰地展现数据的特征,包括数据的形态、异常值、随时间变化情况以及变量间的相互关系。我们在预测时应尽可能地将图中显示的特征纳入考虑。正如数据类型决定使用什么预测方法一样,数据类型也决定了使用什么图形来展示数据。
在画图之前,首先我们应该在R中设置我们的时间序列数据。
ts 对象
R语言中的一种记录时序的对象。
y <- ts(c(123,39,78,52,110), start=2012)
时间图
对于时间序列数据而言,我们从最简单的时间图开始。时间图是用将观测值与观测时间点作图,散点之间用直线连接。例如图2.1表示在澳大利亚两个最大的城市之间,Ansett航空公司的每周客流量。
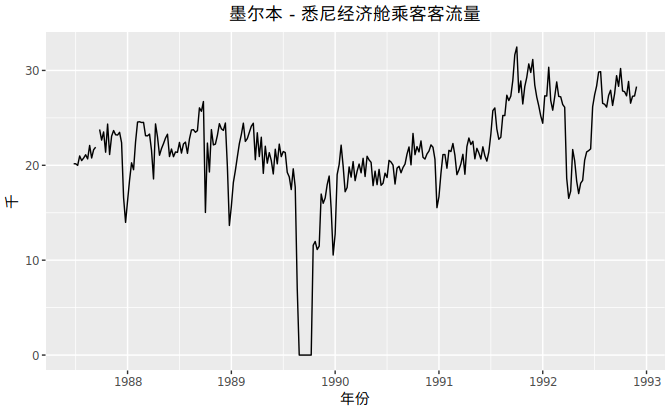
该时间图直观地展现出数据具有的一些特征:
- 由于1989年当地的工业纠纷,当年的客流量为0.
- 在1992年中,由于一部分经济舱被商务舱取代,导致客流量大幅减少。
- 1991年下半年客流量大幅上升。
- 由于假日效应,在每年年初,客流量都会有一定幅度的下降。
- 这是序列存在长期波动,在1987年向上波动,在1988年向下波动,而在1990年和1991年又再次向上波动。
- 在某些时期存在缺失值。
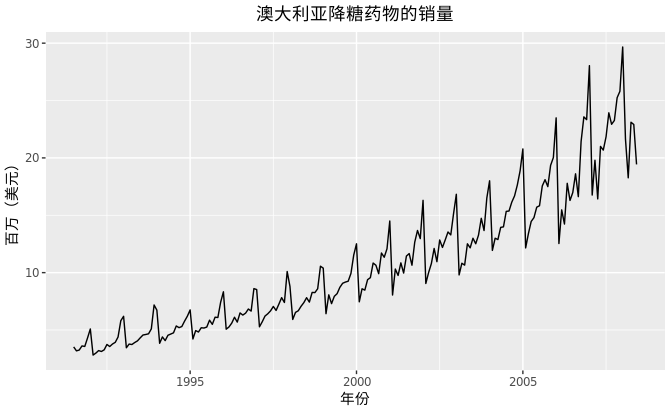
- 显然,图示的时间序列具有明显增长的趋势。
- 同时,在上升趋势中伴随着明显的季节性。
- 在每年年底,由于政府补贴计划,使得降糖药品更便宜,所以人们倾向于在年底囤积药物,从而导致年初的销售额大幅下降。
- 因此,当我们对降糖药物的销量进行预测时,需同时考虑其趋势和季节性因素。
时间序列形态
我们通常使用例如“趋势”、“季节性”等词语描述时间序列。在深入研究时间序列形态时,应该更精确的定义这些词语。
趋势
当一个时间序列数据长期增长或者长期下降时,表示该序列有 趋势 。在某些场合,趋势代表着“转换方向”。例如从增长的趋势转换为下降趋势。在图 2.2 中,明显存在一个增长的趋势。
季节性
当时间序列中的数据受到季节性因素(例如一年的时间或者一周的时间)的影响时,表示该序列具有 季节性 。季节性总是一个已知并且固定的频率。由于抗糖尿病药物的成本在年底时会有变化,导致上述抗糖尿药物的月销售额存在季节性。
周期性
当时间序列数据存在不固定频率的上升和下降时,表示该序列有 周期性 。这些波动经常由经济活动引起,并且与“商业周期”有关。周期波动通常至少持续两年。
许多初学者都不能很好的区分季节性和周期,然而这两个概念是完全不同的。当数据的波动是无规律时,表示序列存在周期性;如果波动的频率不变并且与固定长度的时间段有关,表示序列存在季节性。一般而言,周期的长度较长,并且周期的波动幅度也更大。
许多时间序列同时包含趋势、季节性以及周期性。当我们选择预测方法时,首先应该分析时间序列数据所具备的特征,然后再选择合适的预测方法抓取特征。
以下四个示例分别是上述三个特征的不同组合。
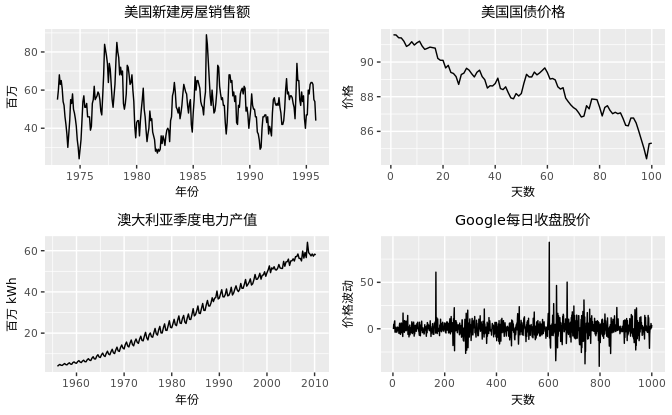
- 美国新建房屋销售额(左上)表现出强烈的年度季节性,以及周期为6~10年的周期性。但是数据并没有表现出明显的趋势。
- 美国国债价格(右上)表示1981年美国国债在芝加哥市场连续100个交易日的价格。可以看出,该序列并没有季节性,但是有明显下降的趋势。假如我们拥有该序列更多的观测数据,我们可以看到这个下降的趋势是一个长期循环的一部分。但是现在我们只有连续100天的数据,它表现出下降的趋势。
- 澳大利亚月度电力产值数据(左下)明显表现出向上增长的趋势,以及强季节性。但是并不存在周期性。
- Google收盘股价格(右下)的价格波动没有趋势,季节性和周期性。随机波动没有良好的形态特性,不能很好地预测。
季节图
季节图和时间序列图很相似,不同之处是季节图是针对观察数据的“季节性”绘制的。下面的例子是降糖药物的销售情况。
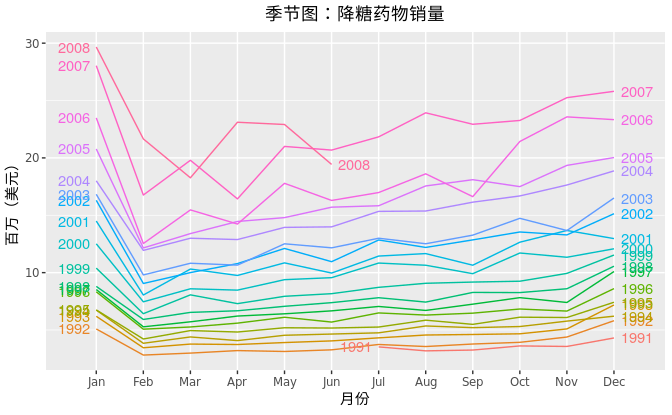
在早些年,数据形态基本相同,但是近些年数据存在相互堆叠的情况。季节图可以很清晰的显示季节形态,这对识别数据形态是否发生变化非常有效。
在本例中,在每年一月份降糖药物的销量都会大幅下降。实际上,患者会在12月下旬大量购买降糖药物,但是这部分销量会在一两周后才向政府登记。从上图还可以看出,2008年3月销量大幅下降(其他年份2月份至3月份的销量增加)。2008年6月份销量较少可能是由于销量数据收集不完整导致。
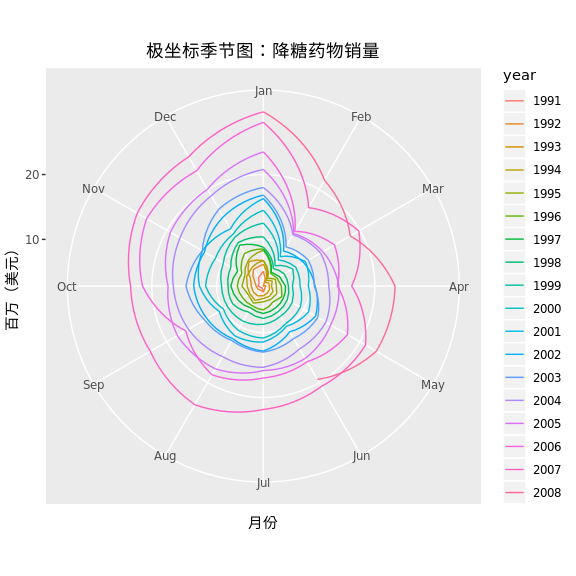
季节图中可以将直角坐标转换为极坐标。
子系列季节图
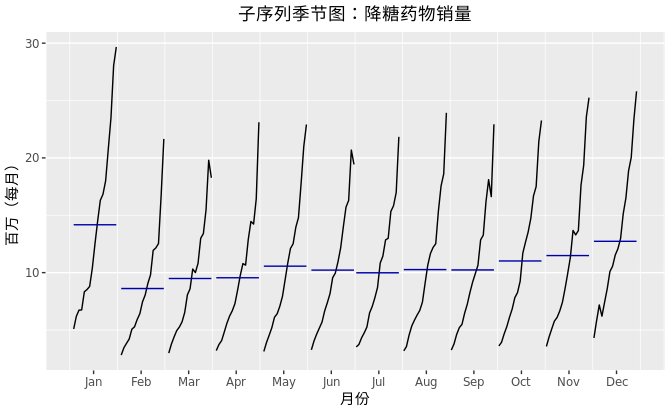
图中的水平线表示每月的平均销量。子系列季节图可以清晰的描绘出数据的潜在季节性形态,并且显示了季节性随时间的变化情况。这类图可以很好地查看各时期内数据的变化情况。在本例中,子系列季节图并没有明显地体现数据特性,但是这是观察季节性变化最有用的方式。
散点图
在此之前,我们所讨论的内容都是单个时间序列的可视化。此外,多个时间序列的可视化也是非常有用的。 图 2.7 分别展示了两个时间序列:2014年澳大利亚维多利亚州每半小时的用电量(以千兆瓦为单位)和温度(以摄氏度为单位)
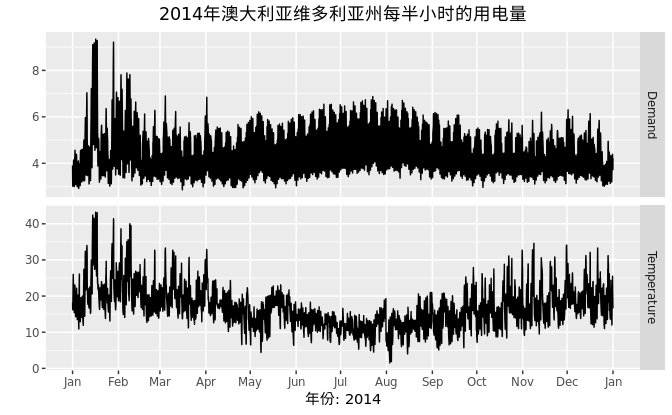
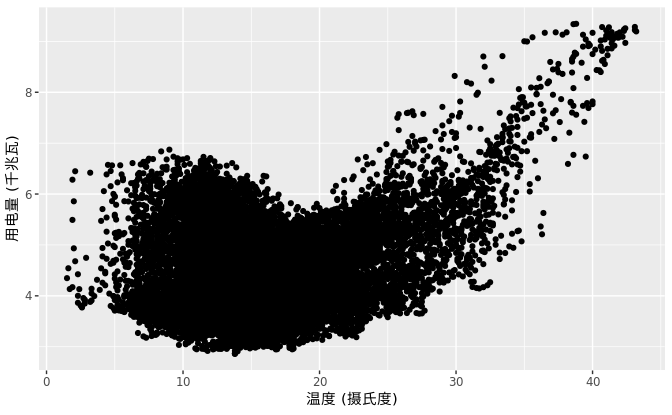
这个散点图可以很好的帮助我们理解变量之间的相互关系。从图中我们可以看出,当温度很高时,人们会大量的使用空调进行降温,进而导致用电量随之增加;当温度很低时,人们会使用空调取暖,也会使得用电量一定程度上增加。
相关性
我们经常会用 相关系数 衡量两个两个变量之间的相关强度。假如已知两个变量 x 和 y ,那么它们之间的相关系数为:
r 的值始终在-1到1之间。当两个变量完全负相关时,r 值为-1;当两个变量完全正相关时,r 为1.图 2.9 分别展示了不同相关强度的例子。
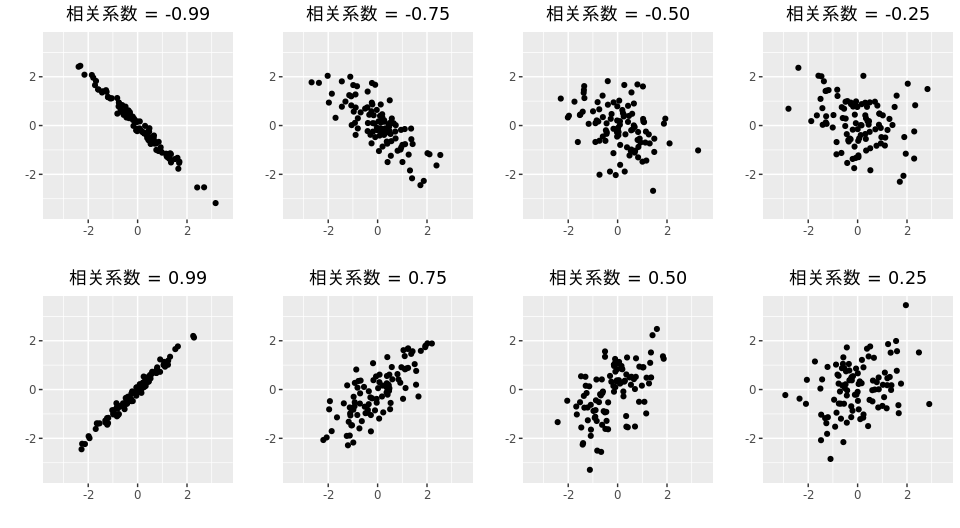
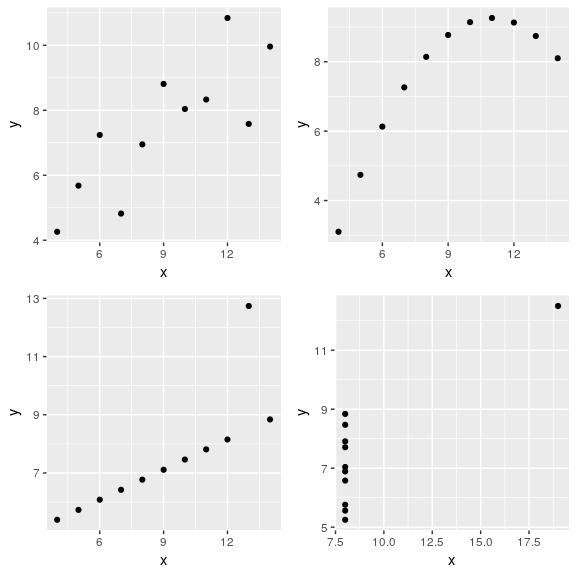
需要注意的是,相关系数仅仅衡量了变量之间的线性关系,并且有时会导致错误的结果。例如,在图 2.10中,所有例子的相关系数均为0.82,但是它们有着完全不同的形态。 这表明,在分析变量之间关系时,不仅要看相关系数值,而且要关注生成的图形。
在图 2.8中,用电量和温度之间的相关系数仅为0.2798,但并不代表用电量和温度之间存在很强的非线性关系。
散点图矩阵
当所分析的数据有多个变量时,将每个变量与其他变量进行比较也很有意义。如图2.11所示,表示澳大利亚新南威尔士五个地区的季度游客人数。
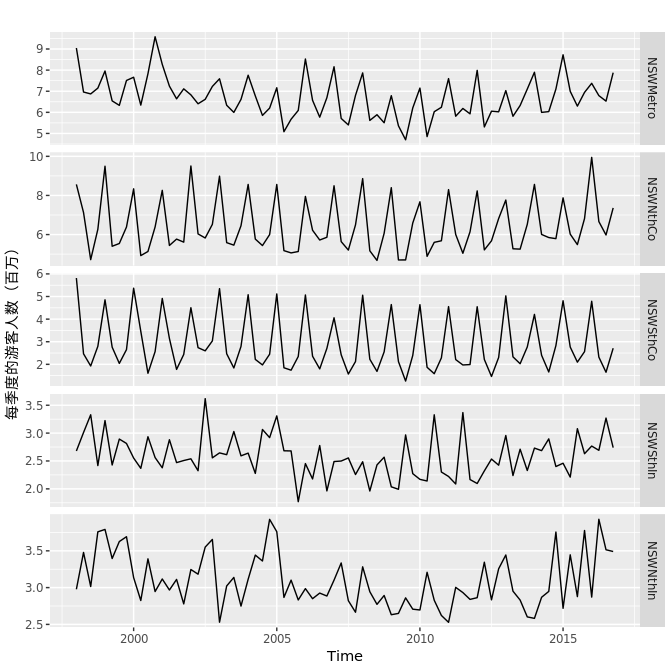
如图 2.12所示,我们可以绘制出它们的散点图矩阵。
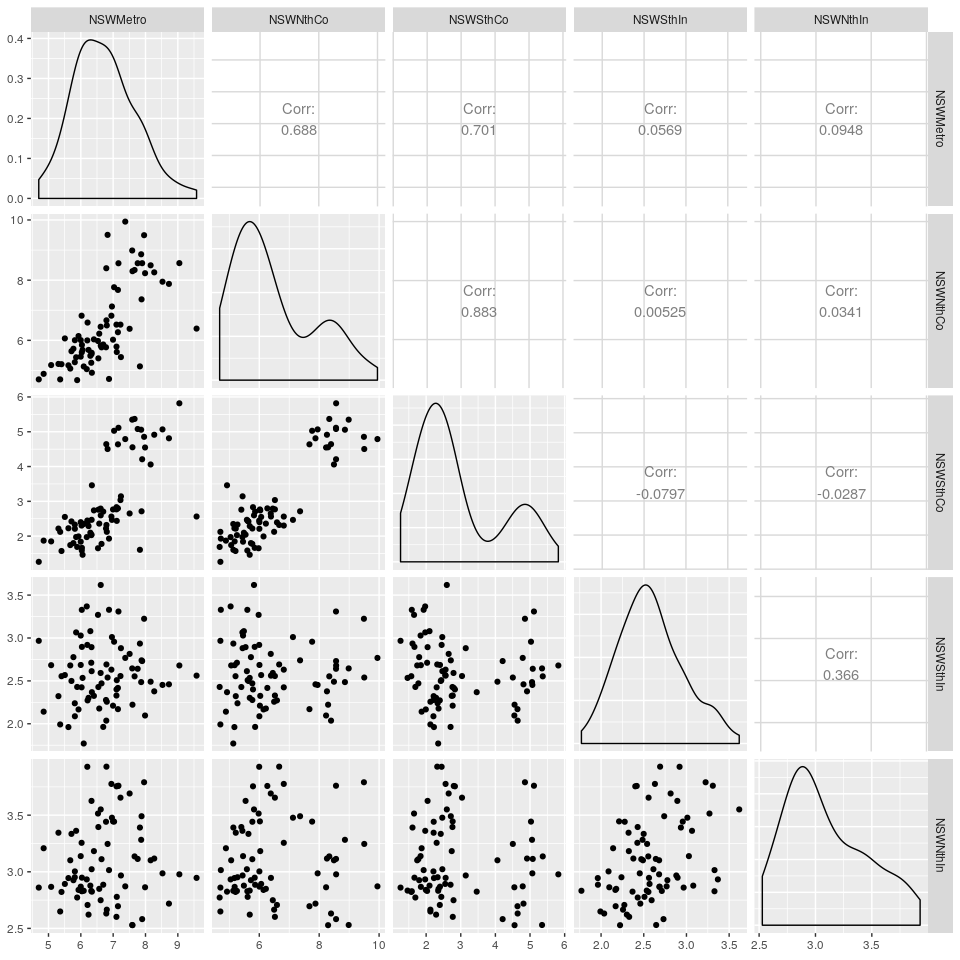
我们可以通过散点图矩阵快速查看所有变量之间的相关关系。在本例中,由图中第二列数据可知,新南威尔士州北部海岸游客与新南威尔士南部海岸游客之间存在强烈的正关系,而新南威尔士州北部海岸的游客与新南威尔士内陆游客之间几乎没有相关关系。同时,我们可以通过散点图矩阵检测到异常值。由于2000年悉尼奥运会,新南威尔士大都会地区存在异常大的客流量。
滞后图
图 2.13是澳大利亚每季度啤酒产量的散点图,横轴表示时间序列的滞后阶数。各图分别显示了不同 k 值下 $ y _{t} $ 和 $ y _{t-k} $ 的散点图。
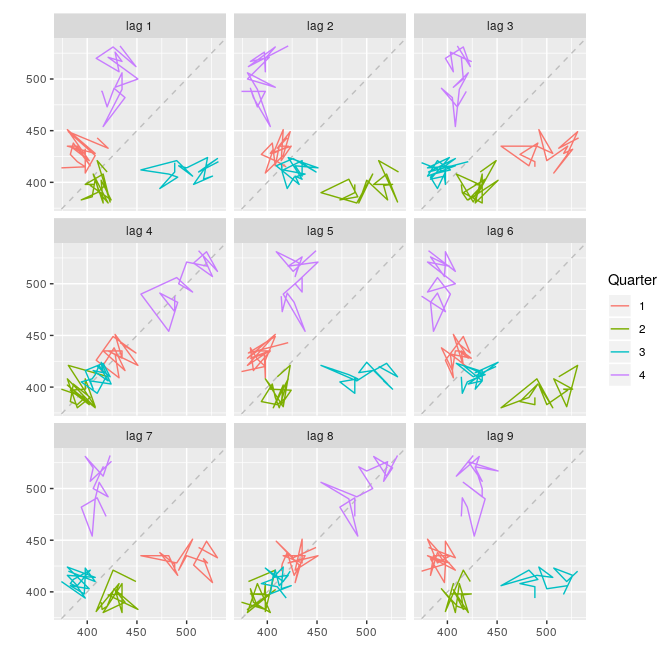
2-13 澳大利亚每季度啤酒产量不同滞后阶数散点图
图中不同颜色代表不同季节,每条线都按时间顺序连接。从图中可以看出,滞后四阶和滞后八阶有正相关关系,说明数据具有很强的季节性。二阶滞后图和六阶滞后图显示,第四季度的峰值对应第二季度的最低点。
自相关
正如相关系数可以衡量两个变量之间的线性相关关系一样,自相关系数可以测量时间序列 滞后值 之间的线性关系。
以下几个不同的自相关系数,对应于滞后图中的不同情况。例如, $ r _{1} $ 衡量 $ y _{t} $ 和 $ y _{t-1} $ 之间的关系, $ r _{2} $ 衡量 $ y _{t} $ 和 $ y _{t-2} $ 之间的关系.
其中, $ r _{k} $ 的定义如下:
其中,T 是时间序列的长度。
澳大利亚啤酒产量数据的前九个自相关系数如下表所示。(略)
各值分别对应于图 2.13 中的九个散点图。通过绘制自相关系数图可以描绘 自相关函数 或者是ACF。因此也被称为相关图。
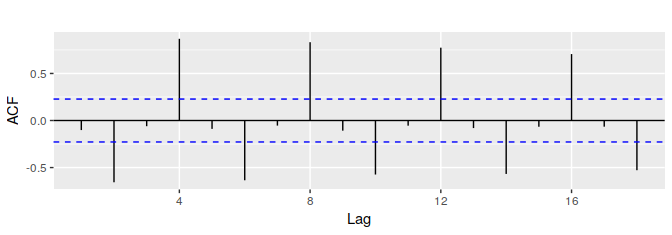
在该图中:
- $ r _{4} $ 值最大。这是由于数据的季节性形态:顶峰往往出现在第四季度,谷底往往出现在第二季度。
- $ r _{2} $ 值最小。这是由于谷底往往在高峰之后的两个季度出现。
- 蓝色虚线之内的区域自相关性可近似看做0。这将会在下节详细阐述。
ACF 图中的趋势性和季节性
当数据具有趋势性时,短期滞后的自相关值较大,因为观测点附近的值波动不会很大。时间序列的ACF一般是正值,随着滞后阶数的增加而缓慢下降。
当数据具有季节性时,自相关值在滞后阶数与季节周期相同时(或者在季节周期的倍数)较大。
当数据同时具有趋势和季节性时,我们会观察到组合效应。如图 2.15 是澳大利亚用电量,该序列同时具有趋势和季节性。它的ACF值如图 2.16 所示。
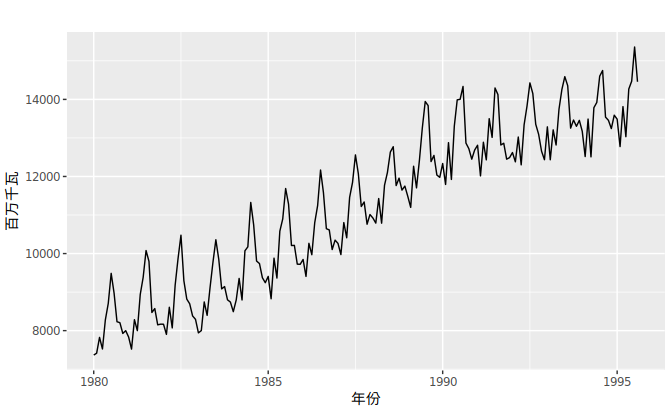

自相关系数值随着滞后阶数增加而缓慢降低,是因为原时间序列中具有趋势变化,而图中的“圆齿状”形状是来源于原时间序列中的季节性变化。
白噪声
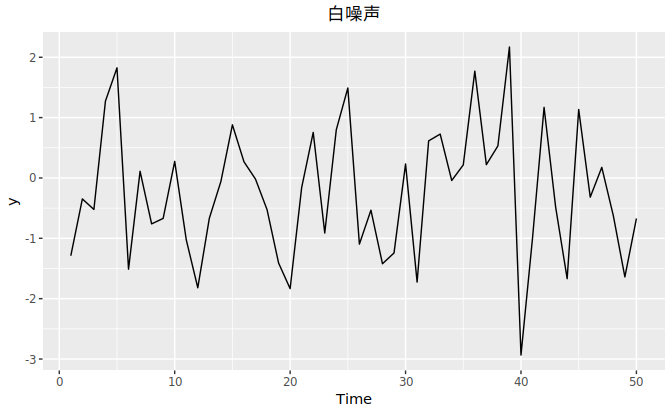
“白噪声”是一个对所有时间其自相关系数为零的随机过程。 图 2.17是一个白噪声的例子。
白噪声函数的自相关函数如下图所示:
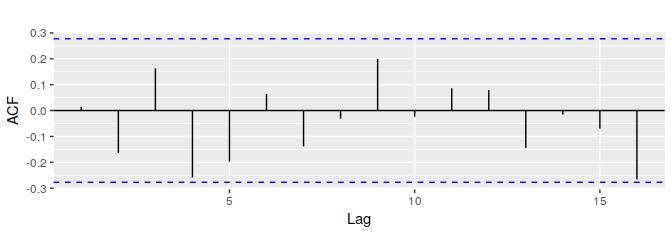
对于白噪声而言,我们期望它的自相关值接近0。但是由于随机扰动的存在,自相关值并不会精确地等于0。对于一个长度为 T 的白噪声序列而言,我们期望在0.95的置信度下,它的自相关值处于 $ \pm 2/\sqrt{T} $ 之间。我们可以很容易的画出ACF的边界值(图中蓝色虚线)。如果一个序列中有较多的自相关值处于边界之外,那么该序列很可能不是白噪声序列。
在上例中,序列长度 T = 50,边界为 $ \pm 2/\sqrt{50} = \pm 0.28 $ 。所有的自相关值均落在边界之内,证明序列是白噪声.
拓展阅读
- Cleveland (1993) 是关于数据分析可视化原理的经典著作。虽然已有20多年历史,但它的思想永不过时。
- Unwin (2015) 是一本关于使用R进行图形数据分析的前沿著作。它并没有着重介绍如何绘制时间序列图形,更多的是关于使用图形进行数据分析。