引言
凸优化之所以如此重要,是因为凸优化的重要特性:凸优化的任意局部最优解也是全局最优解
数学优化
数学优化问题定义(1.1):
$$minimize\ f_{0}(x)$$
$$subject\ to\ f_{i}(x)<=b_{i}, i=1,…,m$$
- 其中,向量$x=(x_{1},x_{2},…,x_{n})$称为问题的优化变量
- 函数$f_{0}:R^{n}\rightarrow R$称为目标函数
- 函数$f_{i}:R^{n}\rightarrow R,\ i=1,…,m$称为(不等式)约束函数
- 常数$b_{1},…,b_{m}$称为约束上限或者约束边界
对于任意满足约束$f_{1}(z)<=b1,…,f_{m}(z)<=b_{m}$的向量$z$,有$f_{0}(z)>=f_{0}(x^{})$,那么称$x^{}$为上述问题的最优解.
线性规划(1.2):
若优化问题(1.1)中的目标函数和约束函数$f_{0},…,f_{m}$都是线性函数,即对任意的$x,y\in R^{n}$和$\alpha,\beta\in R$有:
$$f_{i}(\alpha x+\beta y)=\alpha f_{i}(x)+\beta f_{i}(y).$$
则此优化问题称为线性规划,若优化问题不是线性的,则称之为非线性优化。
最小二乘问题
最小二乘问题是其中的一个优化特例,它没有约束条件(即$m=0$),目标函数是若干项的平方和,每一项具有形式$a_{i}^{T}x-b_{i}$,具体形式如下(1.4):
$$minimize\ f_{0}(x)=||Ax-b||{2}^{2}=\sum{i=1}^{k}(a_{i}^{T}x-b_{i})^{2}.$$
- 其中,$A\in R^{k*n}(k>=n)$
- $a_{i}^{T}$是矩阵$A$的行向量
- 向量$x\in R^{n}$是优化变量
求解最小二乘问题:
最小二乘问题(1.4)的求解可以化简为求解一组线性方程:
$$(A^{T}A)x=A^{T}b$$
因此,其解析解为$x=(A^{T}A)^{-1}A^{T}b$.
凸集
仿射集:略
凸集定义:集合$C$被称为凸集,如果$C$中任意两点间的线段任然在$C$中,即对任意$x_{1},x_{2}\ \in C$和满足$0<=\Theta <=1$的$\Theta$都有:
$$\Theta x_{1}\ +\ (1-\Theta)x_{2} \in C$$
粗略地,如果集合中每一点都可以被其他点沿着它们之间一条无阻碍的路径看见,那么这个集合就是凸集。无阻碍是指整条路径都在集合中。
例如:
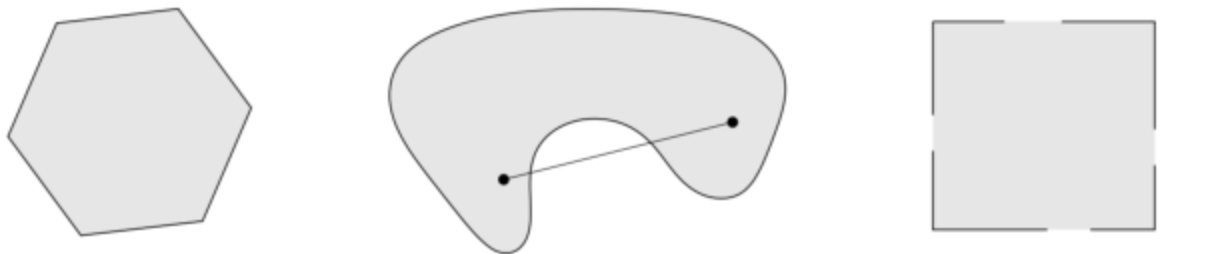
- 第一个:是凸集(集合中的任意两点连线的所有点,都在集合中)
- 第二个:不是凸集,原因图中已经标的很清楚了(有空隙)
- 第三个:不是凸集,有些边没有在集合中
凸函数
凸函数定义:
函数$f:R^{n}\rightarrow R$是凸的,如果$dom\ f$是凸集,且对于任意$x,y \in dom\ f$和任意$0<=\Theta <=1$,有式(3-1):
$$f(\Theta x\ +\ (1-\Theta)y)<=\Theta f(x)+(1-\Theta)f(y)$$

从几何意义上看,上述不等式意味着点$(x,f(x))$和$(y,f(y))$之间的线段,即$x$到$y$的弦,在函数$f$的上方。如果式(3-1)中的不等式$x≠y$以及$0<\Theta <1$是严格成立,则称$f$是严格凸的。
凸函数的性质:
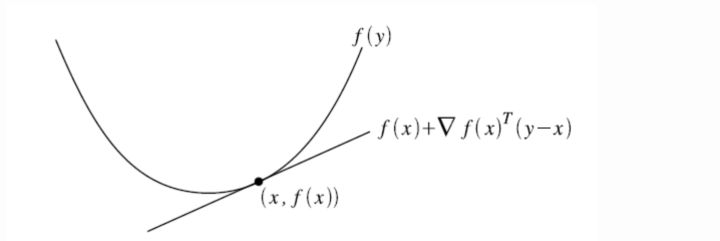
一阶条件
假设$f$是可微的(即其梯度$\bigtriangledown f$在开集$dom\ f$内处处存在),则函数$f$是凸函数的充要条件是:
- (1)$dom\ f$是凸集
- (2)对于任意$x,y\in dom\ f$, 该式成立:$f(y)>=f(x)+ \bigtriangledown f(x)^{T}(y-x).$
二阶条件
假设函数$f$是二阶可微的,即对于开集$dom\ f$内的任意一点,它的$Hessian$矩阵或者二阶导数$\bigtriangledown ^{2}f$存在,则函数$f$是凸函数的充要条件是:
- 其$Hessian$矩阵是半正定阵,即对于所有的$x\in dom\ f$,有$\bigtriangledown ^{2}f(x)>=0$.
- 对于$R$上的函数,上式可以简化为$f^{‘’}(x)>=0$,此条件说明函数$f$的导数是非减的。
我们如果能够判断一个函数的海瑟矩阵是正定的,那么我们就可以说这个函数就是凸函数。判断完了凸函数,我们就可以利用凸函数的性质。
凸优化问题
凸优化问题的标准形式(4.15):
$$minimize\ f_{0}(x)$$
$$subject\ to\ f_{i}(x)<=0,\ i=1,…,m$$
$$a_{i}^{T}x=b_{i},\ i=1,…,p$$
的问题,其中$f_{0},…,f_{m}$为凸函数,$x^{*}\in X$是可微函数$f_{0}$的最优解,当且仅当:
$$\bigtriangledown f_{0}(x^{})^{T}(y-x^{})>=0,y\in X$$
无约束凸优化的问题
问题定义
无约束凸优化问题(即(4.15)式中,m=p=0),$x^{*}\in X$是可微函数$f$的最优解的重要条件是:
$$\bigtriangledown f(x^{*})=0$$
求解方法
(1) 解析解
对于少数一些简单的凸优化问题,可以利用最优性准则通过解析来求解。但对于大多数凸优化问题来讲,是没有办法通过解析来求解的。
(2) 下降方法:确定步长、确定搜索方向.

(3) 确定步长的方法:固定步长搜索、精确直线搜索、回溯直线搜索
(4) 确定搜索方向的方法:梯度下降方法、最速下降方法(一阶泰勒展开近似优化)、牛顿法(二阶泰勒展开近似优化).
- 梯度下降方法必须满足:搜索方向和负梯度成锐角,简单方法是直接用负梯度作为搜索方向,即
$$\Delta x=-\bigtriangledown f(x)$$
- 最速下降方法(一阶泰勒展开近似优化)

- 牛顿法(二阶泰勒展开近似优化)



只含等式约束凸优化的问题
问题定义
考虑只含等式约束而没有不等式约束的问题,即
$$minimize\ f_{0}(x)$$
$$subject\ to\ Ax=b,$$
可行解$x$的最优性条件为:对任意满足$Ay=b$的$y$:$\bigtriangledown f_{0}(x)^{T}(y-x)>=0$都成立。
对应的,$x^{*}\in X$是可微函数$f$的最优解的重要条件为,存在$v\in R^{p}$,使得:
$$\bigtriangledown f(x^{*})+A^{T}v=0$$
其中,$A\in R^{p*n}.$
求解方法
通过Lagrange对偶问题求解
不等式约束凸优化的问题
问题定义
$$minimize\ f_{0}(x)$$
$$subject\ to\ f_{i}(x)<=0,\ i=1,…,m$$
$$a_{i}^{T}x=b_{i},\ i=1,…,p$$
其中$f_{0},…,f_{m}$为凸函数。
求解方法
通过Lagrange对偶问题求解:
(1) 原始问题



(2) 对偶问题

(3) 原始问题和对偶问题的关系



